相關(guān)正態(tài)變量情況下可靠性試驗(yàn)靈敏度分析的Monte Carlo法及自適應(yīng)超球重要抽樣法

第二章和第三章討論了重要抽樣法和改進(jìn)重要抽樣法進(jìn)行可靠性試驗(yàn)靈敏度分析的效率和收斂性問題,，重要抽樣法由于將抽樣的密度中心移到了對可靠性試驗(yàn)靈敏度貢獻(xiàn)較大的區(qū)域而提高了抽樣效率,，加快了可靠性試驗(yàn)靈敏度估計(jì)的收斂速度[1],，但目前還缺乏重要抽樣密度中心的穩(wěn)健確定方法,?；诔虻闹匾闃臃?/span>[2]通過在安全域內(nèi)引入一個(gè)超球,，減少了超球內(nèi)極限狀態(tài)函數(shù)的計(jì)算次數(shù)，從而提高了方法的分析效率,。

原則上基于超球的重要抽樣法并不需要有關(guān)設(shè)計(jì)點(diǎn)的信息,，只要保證引入的超球處于安全域內(nèi)，則該方法即可收斂于真實(shí)解,。但是既要使失效域處于超球以外的區(qū)域來保證可靠性試驗(yàn)靈敏度分析的準(zhǔn)確性,，又要使引入的超球盡可能的大來保證可靠性試驗(yàn)靈敏度分析的高效性，就要通過優(yōu)化算法決定超球的較優(yōu)半徑,，此較優(yōu)半徑為標(biāo)準(zhǔn)正態(tài)空間中極限狀態(tài)上離原點(diǎn)最近的點(diǎn)(即最可能失效點(diǎn))到原點(diǎn)的距離,，也就是說基于超球的重要抽樣法在實(shí)際運(yùn)用中還是需要最可能失效點(diǎn)的信息的。一次二階矩(FORM)和二次二階矩(SORM)可以高效的求此最小距離,，但是這兩種方法對于復(fù)雜的極限狀態(tài),，例如高度非線性、多設(shè)計(jì)點(diǎn)或者多模式系統(tǒng),，都是不穩(wěn)健的[3,4],。

本章在文獻(xiàn)[5]自適應(yīng)超球重要抽樣思想的基礎(chǔ)上，提出了一種高效的自適應(yīng)方法，該方法在抽樣的過程中搜集極限狀態(tài)和失效域的信息,，并利用這些信息指導(dǎo)抽樣域越來越接近最可能失效點(diǎn)附近的重要區(qū)域,，通過逐步迭代搜索的方式來確定較優(yōu)超球半徑，從而最大化地提高了基于超球的重要抽樣法的效率,。

另外,，需指出的是，超球重要抽樣是在獨(dú)立的標(biāo)準(zhǔn)正態(tài)空間中展開的,，而在工程實(shí)際中,，各基本變量往往是相關(guān)的，這種相關(guān)性會對結(jié)構(gòu)的可靠性試驗(yàn)及可靠性試驗(yàn)靈敏度產(chǎn)生顯著的影響[6],。為此,，論文針對結(jié)構(gòu)包含相關(guān)正態(tài)變量的情況提出了采用自適應(yīng)超球重要抽樣法進(jìn)行可靠性試驗(yàn)靈敏度分析的兩種思路，兩種思路均需首先將正態(tài)相關(guān)變量轉(zhuǎn)化成正態(tài)獨(dú)立變量[7,8],，并對其進(jìn)行標(biāo)準(zhǔn)化,，然后在獨(dú)立的標(biāo)準(zhǔn)正態(tài)空間中利用自適應(yīng)策略引入超球來篩選樣本。第一種思路是將篩選后的樣本進(jìn)行反變換得到相關(guān)樣本,，對獨(dú)立正態(tài)樣本的篩選也就是對相關(guān)正態(tài)樣本的篩選,，最后即可利用篩選得到的相關(guān)樣本直接進(jìn)行可靠性試驗(yàn)靈敏度分析，將這種方法稱之為直接法,；第二種思路是在獨(dú)立的標(biāo)準(zhǔn)正態(tài)空間中篩選完樣本后，利用篩選后的獨(dú)立樣本求得獨(dú)立正態(tài)變量情況下的可靠性試驗(yàn)靈敏度,，最后依據(jù)相關(guān)變量分布參數(shù)與等效變換后獨(dú)立變量分布參數(shù)之間的關(guān)系,，利用復(fù)合函數(shù)求導(dǎo)公式來求得相關(guān)正態(tài)變量情況下的可靠性試驗(yàn)靈敏度，將這種方法稱之為轉(zhuǎn)換法,。

本章分別采用上述兩種思路并結(jié)合高效的自適應(yīng)策略對含相關(guān)正態(tài)變量的結(jié)構(gòu)進(jìn)行可靠性試驗(yàn)靈敏度分析,，大量廣泛應(yīng)用的單模式和多模式算例的可靠性試驗(yàn)靈敏度分析結(jié)果表明：對于分析含正態(tài)相關(guān)變量的結(jié)構(gòu)的可靠性試驗(yàn)靈敏度問題，所提的兩種基于自適應(yīng)超球重要抽樣的可靠性試驗(yàn)靈敏度分析方法均是高效,、穩(wěn)健,、準(zhǔn)確的。

2.1 相關(guān)正態(tài)變量的獨(dú)立變換[7,8]

由于非正態(tài)變量可以等價(jià)轉(zhuǎn)化為正態(tài)變量,，因此為簡單起見,，本文只討論正態(tài)基本隨機(jī)變量的情況。n維相關(guān)正態(tài)基本隨機(jī)變量的密度函數(shù)如下所示

其中

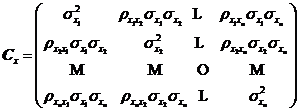
為的協(xié)方差矩陣,，是其逆矩陣,，為該矩陣的行列式值。為的均值向量,，為的標(biāo)準(zhǔn)差,，為和的相關(guān)系數(shù)。

依據(jù)線性代數(shù)的基本原理，對于式定義的n維相關(guān)正態(tài)概率密度函數(shù),，必然存在一個(gè)正交矩陣,，使對于n維隨機(jī)變量有

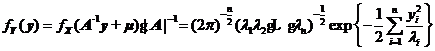
其中，為協(xié)方差矩陣的特征根,。

由上式容易看出隨機(jī)變量服從正態(tài)分布且相互獨(dú)立,，并有

其中的均值向量、方差向量,。

由式引入的線性變換就將相關(guān)正態(tài)隨機(jī)變量等價(jià)地轉(zhuǎn)換為獨(dú)立正態(tài)隨機(jī)變量,。

2.2 相關(guān)正態(tài)變量情況下可靠性試驗(yàn)靈敏度分析的兩種Monte Carlo數(shù)字模擬法

2.2.1 相關(guān)正態(tài)變量情況下可靠性試驗(yàn)靈敏度定義

假設(shè)含n維相關(guān)正態(tài)基本隨機(jī)變量結(jié)構(gòu)的極限狀態(tài)函數(shù)為，則結(jié)構(gòu)的失效域,。依據(jù)失效概率的定義,，相關(guān)正態(tài)變量情況下的失效概率可表示為失效域的指示函數(shù)與的聯(lián)合概率密度函數(shù)的乘積在維實(shí)數(shù)空間中的積分，如式所示,。

其中具有兩個(gè)取值,，當(dāng)時(shí)，,，否則,。

與獨(dú)立變量情況類似，變量相關(guān)情況下的可靠性試驗(yàn)靈敏度定義為失效概率對基本變量分布參數(shù)的偏導(dǎo)數(shù),，以(對于相關(guān)正態(tài)變量,，表示、和)記第i個(gè)基本變量的分布參數(shù),，可得對的可靠性試驗(yàn)靈敏度如式所示,。

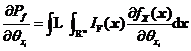
以下將建立兩種基于Monte Carlo數(shù)字模擬的相關(guān)正態(tài)變量情況下的可靠性試驗(yàn)靈敏度分析方法，其一是直接法,，其二是轉(zhuǎn)換法,。

2.2.2 相關(guān)正態(tài)變量情況下基于Monte Carlo數(shù)字模擬的可靠性試驗(yàn)靈敏度分析的直接法

2.2.2.1 相關(guān)正態(tài)變量情況下基于Monte Carlo直接法的可靠性試驗(yàn)靈敏度估計(jì)值

如第二章所述，引入相關(guān)變量的密度函數(shù)為抽樣概率密度函數(shù),，則式的可靠性試驗(yàn)靈敏度可轉(zhuǎn)化為式所示的數(shù)學(xué)期望的形式,。

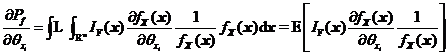
其中表示以為密度函數(shù)的數(shù)學(xué)期望算子。

以為抽樣密度函數(shù)抽取個(gè)相關(guān)的正態(tài)樣本點(diǎn),，并以樣本均值來估計(jì)式所示的數(shù)學(xué)期望形式的可靠性試驗(yàn)靈敏度,，可得相關(guān)正態(tài)變量情況下可靠性試驗(yàn)靈敏度估計(jì)值如下式所示。

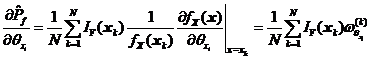
其中,。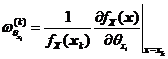

對于式所示的相關(guān)正態(tài)概率密度函數(shù),，當(dāng)、和時(shí),，可分別求得,、和如式~所示,。

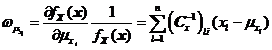
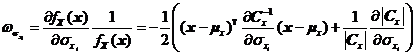
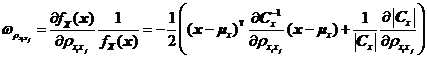
其中表示協(xié)方差矩陣的逆矩陣的第行第列的元素。

將式~分別代入到式中,，可得失效概率對變量均值,、標(biāo)準(zhǔn)差及相關(guān)系數(shù)的可靠性試驗(yàn)靈敏度估計(jì)值、及分別如式~所示,。

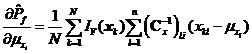
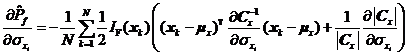
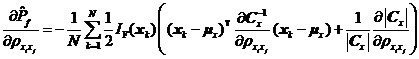
其中為第k個(gè)樣本點(diǎn)的第l個(gè)分量,。

2.2.2.2 相關(guān)正態(tài)變量情況下基于Monte Carlo直接法的可靠性試驗(yàn)靈敏度估計(jì)值的方差分析

采用式所示的樣本均值來估計(jì)數(shù)學(xué)期望是近似的，隨著樣本容量的增大,，式的估計(jì)值收斂于式的真值,。為了對式估計(jì)值的收斂性有所了解，有必要對估計(jì)值作方差分析,。對式所示的估計(jì)值求數(shù)學(xué)期望,，可得式，在忽略樣本間的相關(guān)性時(shí),，可近似求得式估計(jì)值的方差如式所示,。

顯然，是可靠性試驗(yàn)靈敏度的無偏估計(jì),。

在數(shù)值模擬的過程中,，考慮用樣本平均值和方差分別代替總體的數(shù)學(xué)期望和方差，可近似得到靈敏度估計(jì)值的數(shù)學(xué)期望和方差分別如下所示,。

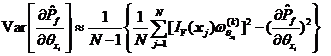
變異系數(shù)為估計(jì)值的標(biāo)準(zhǔn)差與估計(jì)值均值的比值,，反映了估計(jì)值的相對分散性，相關(guān)正態(tài)變量情況下基于Monte Carlo直接法的可靠性試驗(yàn)靈敏度估計(jì)值的變異系數(shù)如下,。

2.2.3 相關(guān)正態(tài)變量情況下基于Monte Carlo數(shù)字模擬的可靠性試驗(yàn)靈敏度分析的轉(zhuǎn)換法

2.2.3.1 相關(guān)正態(tài)變量情況下基于Monte Carlo轉(zhuǎn)換法的可靠性試驗(yàn)靈敏度估計(jì)值

對于相關(guān)正態(tài)變量情況下的可靠性試驗(yàn)靈敏度分析問題,，Monte Carlo轉(zhuǎn)換法的基本思想是：首先按照第4.1節(jié)所示的方法將相關(guān)的正態(tài)變量等價(jià)地轉(zhuǎn)換成獨(dú)立的正態(tài)變量，然后在變換后的獨(dú)立正態(tài)空間中求得獨(dú)立變量情況下的可靠性試驗(yàn)靈敏度估計(jì)值,，最后再利用空間分布參數(shù)與空間分布參數(shù)的轉(zhuǎn)換關(guān)系，由復(fù)合函數(shù)求導(dǎo)法則將求得的估計(jì)值轉(zhuǎn)換到相關(guān)空間,，即可得到相關(guān)正態(tài)變量情況下的可靠性試驗(yàn)靈敏度估計(jì)值,。

（1）獨(dú)立空間中基于Monte Carlo模擬的可靠性試驗(yàn)靈敏度的估計(jì)值

按照第4.1節(jié)的方法將相關(guān)正態(tài)變量獨(dú)立化后，可以得到獨(dú)立正態(tài)變量的概率密度函數(shù)如下

其中

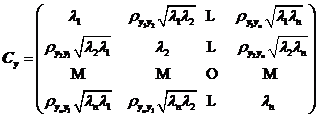
為獨(dú)立正態(tài)變量的協(xié)方差矩陣,，其中的相關(guān)系數(shù),，因此中只有主對角線元素是非零的，而非主對角線元素均為零,。

由相關(guān)正態(tài)空間轉(zhuǎn)換而來的獨(dú)立正態(tài)空間中,，與相關(guān)系數(shù)，作為空間的分布參數(shù),，失效概率對相關(guān)系數(shù)的可靠性試驗(yàn)靈敏度與失效概率對空間的均值,、標(biāo)準(zhǔn)差的靈敏度一樣,，會對最終空間的可靠性試驗(yàn)靈敏度產(chǎn)生影響，因此獨(dú)立的空間中也必須估計(jì)可靠性試驗(yàn)靈敏度,，將寫成式的形式,，就是為了方便估計(jì)。

相關(guān)正態(tài)變量轉(zhuǎn)換成獨(dú)立正態(tài)變量的同時(shí),，空間的極限狀態(tài)函數(shù)也被轉(zhuǎn)換為空間的極限狀態(tài)函數(shù)(為表達(dá)簡單仍記為g),。在轉(zhuǎn)換后的獨(dú)立空間中，結(jié)構(gòu)的失效域?yàn)?/span>,。依據(jù)可靠性試驗(yàn)靈敏度的定義,，失效概率對第個(gè)獨(dú)立變量的分布參數(shù)的靈敏度可表示為

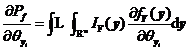
引入n維獨(dú)立的正態(tài)抽樣密度函數(shù)，由2.1節(jié)獨(dú)立正態(tài)變量情況下可靠性試驗(yàn)靈敏度分析的直接Monte Carlo法分析過程可知式可由下式進(jìn)行估算,。

其中,。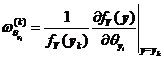

根據(jù)式和可以知道，當(dāng)和時(shí)顯然有下列兩式成立,。

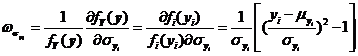
而當(dāng)時(shí),，與式相似的有式成立。

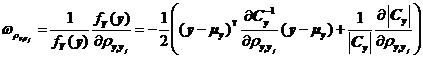
將式~分別代入式中,，可得失效概率對變量均值,、標(biāo)準(zhǔn)差及相關(guān)系數(shù)的可靠性試驗(yàn)靈敏度估計(jì)值、及分別如式~所示,。

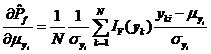
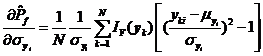
（2）獨(dú)立空間中可靠性試驗(yàn)靈敏度估計(jì)值的方差分析

由于是來自同一母體的獨(dú)立樣本,，因此可求得式估計(jì)值的數(shù)學(xué)期望和方差如下列兩式所示。

類似于式和,，可求得式估計(jì)值的數(shù)學(xué)期望和方差的估計(jì)值如下

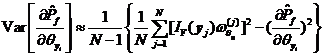
（3）獨(dú)立正態(tài)變量空間可靠性試驗(yàn)靈敏度向相關(guān)正態(tài)變量空間可靠性試驗(yàn)靈敏度的轉(zhuǎn)換

求得獨(dú)立正態(tài)變量空間中的可靠性試驗(yàn)靈敏度估計(jì)值后,，就可根據(jù)變量與的變換關(guān)系，采用復(fù)合函數(shù)求導(dǎo)公式,，將獨(dú)立正態(tài)變量空間中的可靠性試驗(yàn)靈敏度轉(zhuǎn)換到相關(guān)正態(tài)變量空間中的可靠性試驗(yàn)靈敏度,。

由于空間是從空間等價(jià)變換而得到的，因此依據(jù)復(fù)合函數(shù)求導(dǎo)法則,，可由空間的可靠性試驗(yàn)靈敏度估計(jì)值得到空間的可靠性試驗(yàn)靈敏度估計(jì)值：

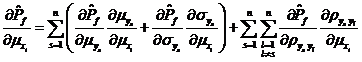
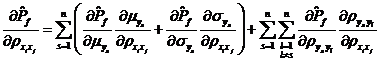
由式~可知,，要利用獨(dú)立正態(tài)變量空間的可靠性試驗(yàn)靈敏度求得相關(guān)正態(tài)變量空間的可靠性試驗(yàn)靈敏度，除了要求得失效概率對空間分布參數(shù)的偏導(dǎo)數(shù)(式~)外,，還必須求得空間分布參數(shù)對空間分布參數(shù)的偏導(dǎo)數(shù),。

根據(jù)式所示的獨(dú)立正態(tài)變量和相關(guān)正態(tài)變量之間的線性關(guān)系可知，的第s個(gè)分量與的各分量,、,、、之間存在如下的線性關(guān)系,。

其中系數(shù)是由相關(guān)正態(tài)變量的協(xié)方差矩陣確定的正交矩陣所決定的常數(shù),。

由上述關(guān)系式可以解析求得獨(dú)立正態(tài)變量的均值,、標(biāo)準(zhǔn)差及相關(guān)系數(shù)與相關(guān)正態(tài)變量的均值、標(biāo)準(zhǔn)差及相關(guān)系數(shù)之間的關(guān)系分別如下所示,。

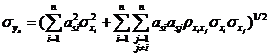
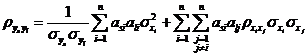
利用式~,，可將獨(dú)立正態(tài)變量空間的分布參數(shù)對相關(guān)正態(tài)變量空間分布參數(shù)的偏導(dǎo)數(shù)全部解析地求出，如式~所示,。

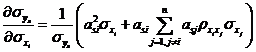
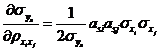
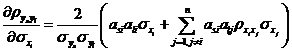
將按照式~求得的獨(dú)立正態(tài)變量空間的可靠性試驗(yàn)靈敏度估計(jì)值和式~求得的代入式~中,，即可求得相關(guān)正態(tài)變量空間中的可靠性試驗(yàn)靈敏度估計(jì)值。

2.2.3.2 相關(guān)正態(tài)變量情況下基于Monte Carlo轉(zhuǎn)換法的可靠性試驗(yàn)靈敏度估計(jì)值的方差分析

在上述基于Monte Carlo數(shù)字模擬求解相關(guān)正態(tài)變量可靠性試驗(yàn)靈敏度的轉(zhuǎn)換法中,，如果在獨(dú)立正態(tài)變量空間中每項(xiàng)可靠性試驗(yàn)靈敏度是采用獨(dú)立的樣本點(diǎn)進(jìn)行計(jì)算的,，那么式~中的估計(jì)值、和均是相互獨(dú)立的,，此時(shí)可由式~所示的與的關(guān)系,，利用獨(dú)立變量和的期望及方差的性質(zhì)來求解相關(guān)正態(tài)變量可靠性試驗(yàn)靈敏度估計(jì)值的數(shù)學(xué)期望和方差，進(jìn)而運(yùn)用式求得可靠性試驗(yàn)靈敏度估計(jì)值的變異系數(shù),。如果在獨(dú)立正態(tài)變量空間中每項(xiàng)可靠性試驗(yàn)靈敏度是采用相同的一組樣本點(diǎn)來估計(jì)時(shí),，則、和之間是相關(guān)的,，此時(shí)求解的數(shù)學(xué)期望與獨(dú)立樣本情況是一致的,，但是求解的方差則較困難，一般可通過控制獨(dú)立正態(tài)空間可靠性試驗(yàn)靈敏度的收斂性來控制的收斂性,，因?yàn)閺?/span>到的轉(zhuǎn)換是解析的,。

2.2.4  Monte Carlo直接法和Monte Carlo轉(zhuǎn)換法的比較

Monte Carlo直接法的優(yōu)點(diǎn)是不需要進(jìn)行可靠性試驗(yàn)靈敏度的轉(zhuǎn)換，因此在求解可靠性試驗(yàn)靈敏度時(shí)更直接,，但直接法需要產(chǎn)生相關(guān)的隨機(jī)樣本,，而一般來說相關(guān)隨機(jī)樣本的產(chǎn)生較獨(dú)立隨機(jī)樣本的產(chǎn)生更困難些。對于正態(tài)相關(guān)隨機(jī)樣本來說,，可以通過獨(dú)立隨機(jī)樣本進(jìn)行變換來得到,。另外直接法中可靠性試驗(yàn)靈敏度估計(jì)值的方差由于樣本點(diǎn)具有相關(guān)性而較難估計(jì)。如果在直接法中選用獨(dú)立的抽樣密度函數(shù),，則可以避免樣本產(chǎn)生的困難以及估計(jì)值方差分析的困難,，但選用獨(dú)立的抽樣密度函數(shù)時(shí)不能與4.3節(jié)的超球重要抽樣法相結(jié)合，不易提高算法的效率,。

Monte Carlo轉(zhuǎn)換法的優(yōu)點(diǎn)是在進(jìn)行相關(guān)正態(tài)變量的可靠性試驗(yàn)靈敏度分析時(shí)不需要產(chǎn)生相關(guān)樣本點(diǎn)。在獨(dú)立的正態(tài)空間中求得可靠性試驗(yàn)靈敏度的估計(jì)值后,，經(jīng)過解析變換即可求得相關(guān)正態(tài)變量空間的可靠性試驗(yàn)靈敏度,，而且獨(dú)立正態(tài)空間的可靠性試驗(yàn)靈敏度估計(jì)值的方差分析較容易。缺點(diǎn)是它必須求得獨(dú)立正態(tài)空間的分布參數(shù)對相關(guān)正態(tài)空間分布參數(shù)的導(dǎo)函數(shù),，但由于此求導(dǎo)是解析的,，因此計(jì)算量與直接法相比不會有明顯增加,。另外，需指出的是：在Monte Carlo轉(zhuǎn)換法中,，如果采用相同樣本估計(jì)獨(dú)立空間的可靠性試驗(yàn)靈敏度,，由于每項(xiàng)獨(dú)立空間可靠性試驗(yàn)靈敏度估計(jì)值的相關(guān)性，造成了轉(zhuǎn)換后的可靠性試驗(yàn)靈敏度估計(jì)值方差分析的困難,，因此在轉(zhuǎn)換后控制估計(jì)值的收斂性是不易實(shí)現(xiàn)的,，此時(shí)必須在獨(dú)立空間中控制可靠性試驗(yàn)靈敏度估計(jì)值的收斂性，以保證解析變換到相關(guān)空間的可靠性試驗(yàn)靈敏度估計(jì)的精度,。

總體上來說,，這兩種Monte Carlo數(shù)字模擬法進(jìn)行相關(guān)正態(tài)變量的可靠性試驗(yàn)靈敏度分析的計(jì)算量相當(dāng)，并且都可以與超球重要抽樣相結(jié)合,，以便進(jìn)一步提高算法的效率,。