可靠性試驗分析的降階積分法

由于非正態(tài)相關(guān)隨機(jī)變量可以轉(zhuǎn)化為正態(tài)獨(dú)立隨機(jī)變量，本章仍主要討論相互獨(dú)立的正態(tài)隨機(jī)變量情況的結(jié)構(gòu)的可靠性試驗靈敏度分析。

假設(shè)所研究問題包含的維基本變量相互獨(dú)立且均服從正態(tài)分布,，，和分別為的均值與標(biāo)準(zhǔn)差。以表示極限狀態(tài)函數(shù),，則結(jié)構(gòu)的失效域。以表示基本變量的聯(lián)合概率密度函數(shù),，則結(jié)構(gòu)的失效概率如式所示,。

首先利用式對變量進(jìn)行標(biāo)準(zhǔn)正態(tài)化

經(jīng)過上式變換后，即為所對應(yīng)的標(biāo)準(zhǔn)正態(tài)化向量,。

一般的,，式中聯(lián)合概率密度函數(shù)比較復(fù)雜，積分上下限也不明確,，特別是在具有多隨機(jī)變量時,，情況變得更復(fù)雜,，使積分求解十分困難。利用獨(dú)立標(biāo)準(zhǔn)正態(tài)變量空間的幾個重要性質(zhì),，將隨機(jī)變量空間的坐標(biāo)軸通過下面的公式轉(zhuǎn)換成極坐標(biāo)形式后,，原來復(fù)雜的積分形式變得比較簡潔而富有規(guī)律。

經(jīng)過坐標(biāo)轉(zhuǎn)換之后,，為了求得具有個隨機(jī)變量的維正交標(biāo)準(zhǔn)正態(tài)空間中超球體域的積分精確值,，文獻(xiàn)[1]采用歸納的方法，先討論低維變量空間的情況,，再得出高維及維變量空間的積分形式,。

3.1.1 單模式的降階積分法

3.1.1.1 二維隨機(jī)變量時可靠性試驗分析的降階積分法

對于相互獨(dú)立的二維隨機(jī)變量，標(biāo)準(zhǔn)正態(tài)化后得到,，,，通過式進(jìn)行極坐標(biāo)轉(zhuǎn)換聯(lián)合概率密度函數(shù)變?yōu)?/span>

把離散為，即,，這樣就把整個坐標(biāo)空間分成個以原點為圓心,、為射線角的扇形，它們與失效邊界的交點處的特征半徑記為,，如圖5.1所示,。記為獨(dú)立的二維標(biāo)準(zhǔn)正態(tài)變量空間中以原點為圓心、半徑為的圓形區(qū)域內(nèi)側(cè)的聯(lián)合概率密度函數(shù)的積分（以下類同）,，則有[1]

圖5.1 單模式的降階積分法示意圖

相應(yīng)的,，記為在上述區(qū)域外側(cè)的概率積分（以下類同），有

假設(shè)結(jié)構(gòu)的失效域為超球外側(cè)的區(qū)域,，則結(jié)構(gòu)的失效概率如式所示,。

其中表示第個微元體對應(yīng)的結(jié)構(gòu)的失效概率，以下類同,。

若結(jié)構(gòu)的失效域為超球內(nèi)側(cè)的區(qū)域,，則結(jié)構(gòu)的失效概率如式所示。

為描述方便起見,，下面均假定結(jié)構(gòu)的失效域為超球體外側(cè)的區(qū)域,，對于失效域為超球體內(nèi)側(cè)區(qū)域的情況可以由式類似地推得。

3.1.1.2 三維隨機(jī)變量時可靠性試驗分析的降階積分法

對于相互獨(dú)立的三維變量,，標(biāo)準(zhǔn)正態(tài)化后得到,，，通過式進(jìn)行極坐標(biāo)轉(zhuǎn)換后聯(lián)合概率密度函數(shù)變?yōu)?/span>

與二維的情況類似,，把,、離散為、,，即,、,，這樣就把三維空間劃分為個以原點為頂點的微棱錐，它們與失效面相交處的特征半徑記為記,。則有

其中為標(biāo)準(zhǔn)正態(tài)分布變量的累積分布函數(shù),。

結(jié)構(gòu)的失效域為超球外側(cè)的區(qū)域時，結(jié)構(gòu)的失效概率如式所示,。

其中為以為半徑的球的表面積,，為以為高度的微棱錐在球面上部分的面積，可分別由式和式求得,。

其中,，、分別為角坐標(biāo)的起始與終了坐標(biāo)值,。

3.1.1.3 其他維數(shù)隨機(jī)變量時可靠性試驗分析的降階積分法

(1) 當(dāng)變量維數(shù)為偶數(shù)時：

(2) 當(dāng)變量維數(shù)為奇數(shù)時：

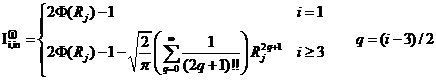
對應(yīng)于可靠性試驗問題,，超球體域外側(cè)為失效域時，結(jié)構(gòu)的失效概率為：

其中為以為半徑的超球的體積,，為以為高度的微元體的體積,。