現(xiàn)有的結(jié)構(gòu)模糊可靠性試驗理論研究中,,通常將模糊可靠性試驗問題轉(zhuǎn)化為常規(guī)可靠性試驗問題來處理,常用的方法有兩類,,第一類是基于![]() 水平截集的方法[1],,第二類是基于模糊隸屬函數(shù)向隨機密度函數(shù)作等價變換的方法[2-3],該方法的適用范圍較廣,,可以應(yīng)用到多個模糊變量的情況,,但這種方法目前還很難解決模糊變量具有非正態(tài)隸屬函數(shù)的可靠性試驗分析問題。
水平截集的方法[1],,第二類是基于模糊隸屬函數(shù)向隨機密度函數(shù)作等價變換的方法[2-3],該方法的適用范圍較廣,,可以應(yīng)用到多個模糊變量的情況,,但這種方法目前還很難解決模糊變量具有非正態(tài)隸屬函數(shù)的可靠性試驗分析問題。
本章采用第二類方法的研究思路,,首先給出了模糊隨機可靠性試驗及可靠性試驗靈敏度分析的數(shù)字模擬方法,。針對基于模糊隸屬函數(shù)向隨機密度函數(shù)作等價變換的方法很難解決非正態(tài)隸屬函數(shù)的情況,本章對模糊變量隸屬函數(shù)為對稱梯形分布的結(jié)構(gòu),,采用了“最大最小”法和“等面積”法,,對模糊變量隸屬函數(shù)為對稱柯西型分布的結(jié)構(gòu),采用了“等面積”法,對模糊變量隸屬函數(shù)為對稱拋物型分布的結(jié)構(gòu),,提出了“改進最大最小”法和“改進等面積”法,,以分別將梯形隸屬函數(shù)、柯西型隸屬函數(shù),、拋物型隸屬函數(shù)近似轉(zhuǎn)化為正態(tài)型隸屬函數(shù),。文中分別給出了上述幾種近似等價正態(tài)化方法的原理及實現(xiàn)步驟,并通過算例比較了幾種方法針對不同分布形式的隸屬函數(shù)在等價正態(tài)化近似程度上的優(yōu)劣,。
假設(shè)![]() 為只具有模糊性的基本變量,,其隸屬函數(shù)為
為只具有模糊性的基本變量,,其隸屬函數(shù)為![]() 。若隸屬函數(shù)
。若隸屬函數(shù)![]() 服從對稱梯形分布,,則
服從對稱梯形分布,,則![]() 的具體形式如式所示[4],其形狀如圖7.1所示,。
的具體形式如式所示[4],其形狀如圖7.1所示,。

其中![]() 為模糊變量
為模糊變量![]() 的中心值,、
的中心值,、![]() 與
與![]() 為其模糊幅度,本文討論
為其模糊幅度,本文討論![]() 為常數(shù)且較小時的情況,,即模糊幅度
為常數(shù)且較小時的情況,,即模糊幅度![]() 與
與![]() 比值較大的情況,。
比值較大的情況,。
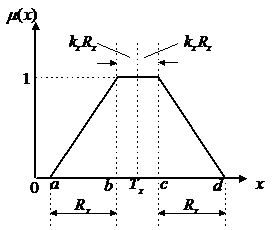
圖7.1 對稱梯形隸屬函數(shù)圖形
若模糊變量![]() 的隸屬函數(shù)
的隸屬函數(shù)![]() 服從對稱柯西型分布,則
服從對稱柯西型分布,則![]() 的具體形式如式所示[4],。
的具體形式如式所示[4],。
![]()
其中![]() >0,、
>0,、![]() 分別為模糊變量
分別為模糊變量![]() 的隸屬函數(shù)的兩個分布參數(shù),
的隸屬函數(shù)的兩個分布參數(shù),![]() 為正偶數(shù),,對于一個給定的隸屬函數(shù)
為正偶數(shù),,對于一個給定的隸屬函數(shù)![]() 為一定值,,僅僅包含
為一定值,,僅僅包含![]() 和
和![]() 兩個參數(shù)。
兩個參數(shù)。
若模糊變量![]() 的隸屬函數(shù)
的隸屬函數(shù)![]() 服從對稱拋物型分布,,則
服從對稱拋物型分布,,則![]() 的具體形式如式所示[4],,其形狀如圖7.2(a)所示。
的具體形式如式所示[4],,其形狀如圖7.2(a)所示。


(a) (b)
圖7.2 對稱拋物型隸屬函數(shù)圖形
當(dāng)b,、c兩點重合時,,隸屬函數(shù)蛻變?yōu)橄率?/font>,其形狀如圖7.2(b)所示,。
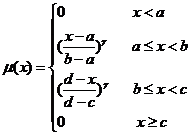
本文主要討論b,、c兩點重合的情況,即圖7.2(b)所示的情況,,此時可選取模糊變量隸屬函數(shù)的兩參數(shù)為:中心值![]() 和模糊幅度
和模糊幅度![]() ,,其幾何意義已在圖7.2(b)中標(biāo)示出。則隸屬函數(shù)可寫成下面的形式
,,其幾何意義已在圖7.2(b)中標(biāo)示出。則隸屬函數(shù)可寫成下面的形式
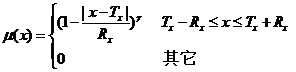
對于一個給定的模糊變量,,隸屬函數(shù)中的![]() 為一個確定值,,僅僅包含中心值
為一個確定值,,僅僅包含中心值![]() 和模糊幅度
和模糊幅度![]() 兩個參數(shù)。
兩個參數(shù)。